Background
Machine learning (ML) methods are used to model complex patterns of behavior in applications where physics-based approaches are computationally intractable or are not feasible because the physics is not fully understood. However, ML models often take large amounts of data to train and cannot be applied outside of the training data space. Physics-informed ML is an emerging class of ML approaches that has the ability to make ML models more generalizable by “informing” the ML algorithm with basic knowledge about the physical system (e.g. constraints, governing equations, boundary conditions). This SwRI IR&D project aims to develop a novel physics-informed ML framework that incorporates governing partial differential equations (PDEs) into the ML loss function to facilitate rapid, physically realistic predictions of stress and strain in a material body with damage (e.g., crack, hole, and notch defects). The hypothesis is that using physics-informed ML for modeling material damage will improve predictions and reduce the amount of training data needed relative to traditional ML approaches. This physics-informed ML approach has the potential to improve predictions of complex and highly irregular damage-induced stress and strain fields in materials and could lead to major advances in life-cycle assessment, material discovery, and design for extreme conditions.
Approach
The physics-informed ML framework being developed in this project uses algorithmic differentiation to incorporate the governing solid mechanics PDEs (i.e., strain-displacement compatibility, stress equilibrium, and the stress-strain constitutive relationship) as additional constraints in a Convolutional Neural Network algorithm. Convolutional Neural Networks are state-of-the-art ML architectures for image processing that learn patterns from the information stored in the pixels of an image. This novel Physics-Informed General Convolutional Network (PIGCN) is being trained using displacement, strain, and stress field images from physics-based finite element simulations of two-dimensional geometries with cracks, holes and notches for a variety of loading and boundary conditions and flaw configurations (e.g., location, orientation, and number of defects). Experimental testing is being performed to validate the PIGCN model predictions. The PIGCN approach will be evaluated by (1) comparing PIGCN displacement, strain, and stress predictions to predictions from a traditional Convolutional Neural Network and (2) determining the training data reduction possible with PIGCN compared to traditional ML.
Accomplishments
To date, the stress equilibrium equation and displacement and traction boundary conditions have been implemented in the PIGCN loss function, and the resulting trained PIGCN model has been used to predict the displacement, strain, and stress fields for a plate with a single hole. Figure 1A shows a comparison of the PIGCN stress predictions to the traditional ML stress predictions for a plate with a single hole. The comparisons in Figures 1B and 1C demonstrate the importance of including the stress equilibrium constraint in the loss function, even for this simple damage configuration of a plate with a hole. As training epochs progress, the equilibrium error converges for the PIGCN stress predictions, but the X and Y equilibrium constraints do not converge and are not minimized using the traditional ML model. Increasing the number of training epochs and the amount of training data do not help the traditional ML model to satisfy the governing equations, indicating that it is necessary to include some of the physics constraints in the loss function to obtain physically consistent predictions. Final project work will include implementation of the strain-displacement compatibility and stress-strain constitutive relationships as constraints in the PIGCN loss function, training with a more diverse set of boundary conditions and flaw configurations, and final model validation.
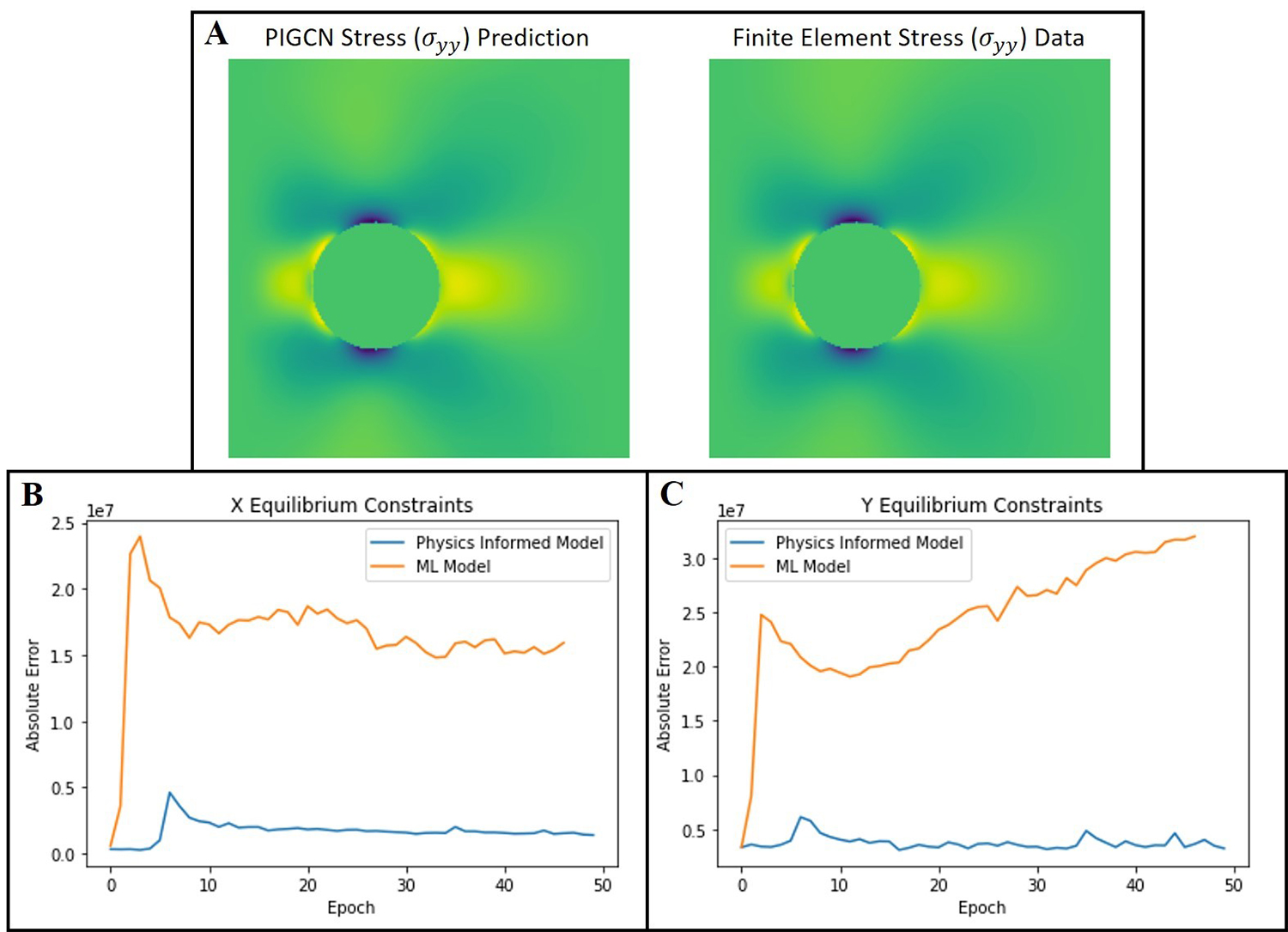
Figure 1: Example of PIGCN predictive capability for stress in a plate with a single hole: (A) Visual comparison of a PIGCN stress prediction (left) compared to an identical finite element model prediction (right) (B) Plot of stress equilibrium in the x-direction for PIGCN (blue) and a traditional Convolutional Neural Network (orange) as a function of number of training epochs. (C) Plot of stress equilibrium in the y-direction for PIGCN (blue) and a traditional Convolutional Neural Network (orange) as a function of number of training epochs.
